MOMENTOS DE INERCIA
MOMENTS OF INERTIA
El momento de inercia o inercia rotacional es una medida de la inercia rotacional de un cuerpo. Más concretamente el momento de inercia es una magnitud escalar que refleja la distribución de masas de un cuerpo o un sistema de partículas en rotación, respecto al eje de giro. El momento de inercia sólo depende de la geometría del cuerpo y de la posición del eje de giro; pero no depende de las fuerzas que intervienen en el cuerpo.
El momento de inercia se relaciona con las tensiones y deformaciones máximas producidas por los esfuerzos de flexión en un elemento estructural, por lo cual este valor determina la resistencia máxima de un elemento estructural bajo flexión junto con las propiedades de dicho material. Para el caso del momento de inercia también depende de cómo esta distribuida la masa. Se encuentra que si la masa está muy concentrada cerca del punto de giro (o eje de rotación) encontramos que esta inercia es menor, pero si está muy alejada del eje es mucho mayor. Lo cierto es que el momento de inercia es un factor importante a considerar en cuanto a la construcción, pues debemos tener conciencia de cómo las vigas (por ejemplo) se comportan en cuanto a la tendencia a girar para tal distribución de masa .
En los cálculos es importante encontrar los valores máximos y mínimos del momento de inercia para tener un control de cómo poner y que viga debemos colocar de acuerdo a lo que se requiere.
El segundo momento de área, o momento de inercia, se define como:
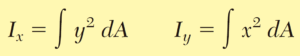
Momento polar de inercia (J)
El momento polar de inercia de un área dada puede calcularse a partir de los momentos rectangulares de inercia Ix e Iy del área, si dichas cantidades ya son conocidas.

Producto de inercia
El producto de inercia del área A respecto a los ejes x y y, se obtiene al multiplicar a cada elemento dA de un área A por sus coordenadas x y y, e integrando sobre toda el área.
A diferencia de los momentos de inercia Ix e Iy, el producto de inercia Ixy puede ser positivo, negativo o cero.
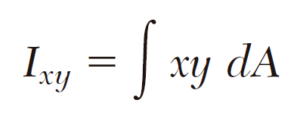
Teorema de ejes paralelos
Esta fórmula expresa que el momento de inercia I de un área con respecto a cualquier eje dado, es igual al momento de inercia I del área con respecto a un eje centroidal que es paralelo al momento de inercia que se desea determinar, más el producto del área A y el cuadrado de la distancia d entre los dos ejes.
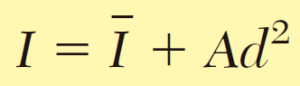
Radio de giro (K)
Se define el radio de giro como la distancia desde el eje de giro a un punto donde podríamos suponer concentrada toda la masa del cuerpo de modo que el momento de inercia respecto a dicho eje se obtenga como el producto de la masa del cuerpo por el cuadrado del radio de giro.
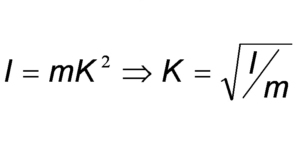
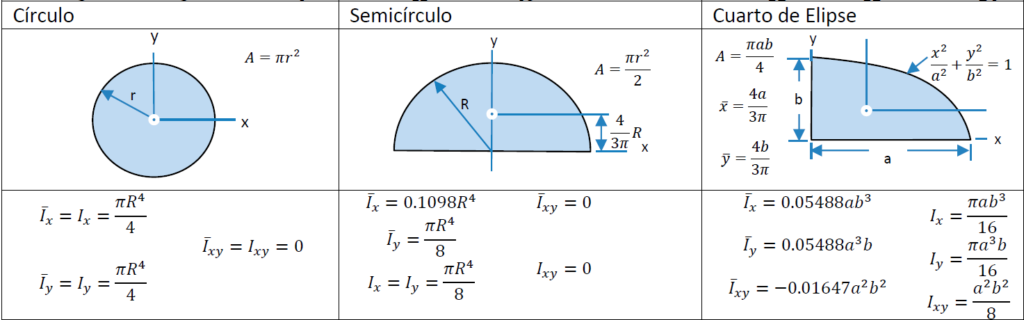
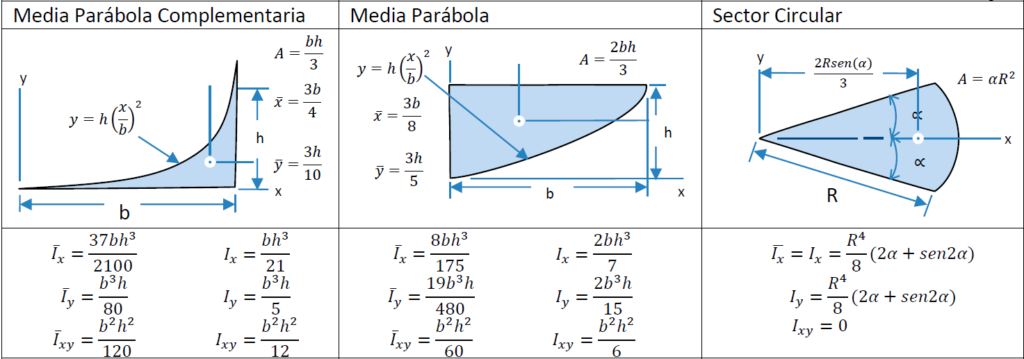
Tabla de centroides y momentos de inercia.


Ejemplo de cálculo de momento de inercia eje horizontal por integración
En el siguiente ejemplo se determina el momento de inercia con respecto al eje x por medio de integrales. Tenemos la ecuación que representa la curva y con ello podemos realizar nuestras operaciones de integración.
Ejemplo de cálculo de momento de inercia eje vertical por integración
En el siguiente ejemplo se determina el momento de inercia con respecto al eje y por medio de integrales. Al igual que con el ejemplo anterior, integraremos de forma horizontal la ecuación que representa la curva y con ello podemos realizar nuestras operaciones de integración.
Ejemplo de cálculo de momento de inercia utilizando tabla
Por medio del uso de la tabla dividimos el cuerpo en elementos geometricos simples. A partir de esto, sumamos los momentos de inercia de cada uno de estos elementos alrededor de un eje común.
Ejemplo de cálculo de momento polar de inercia.
En el siguiente ejemplo se determina el momento polar de inercia. Recordemos que este se puede obtener por medio de la suma de los momentos de inercia del eje vertical y horizontal que pasen por el punto del momento polar. También se puede determinar de forma directa si se conocen las ecuaciones de momento polar.
Ejemplo de cálculo de producto de inercia y ejes paralelos o teorema de Steiner
En el siguiente ejemplo se determina el producto de inercia con respecto a unos ejes dados, para ello se hace uso del teorema de ejes paralelos. El teorema de ejes paralelos también es llamado teorema de Steiner.
Ejemplo de cálculo de la inercia por medio del circulo de Morh
En el siguiente ejemplo se determinan los momentos de inercia y producto de inercia al rotar los ejes por medio del circulo de Morh.