TRASLACION DE FUERZAS - MOMENTO
SISTEMAS EQUIVALENTES DE FUERZAS – EQUIVALENT SYSTEMS OF FORCES.
La traslación de fuerzas es una de las herramientas más utilizadas en la mecánica de sólidos. Esta nos permite poner fuerzas en cualquier parte del cuerpo por fuera de su línea de acción.
Cada vez que trasladamos una fuerza por fuera de su línea de acción aparece un momento.
Mover una fuerza por su línea de acción

Una fuerza se pude mover fácilmente por su línea de acción, esto permite mantener el sistema equivalente sin calcular ningún momento.
Como se puede apreciar en la figura, el sistema de la izquierda es igual al de la derecha. En otras palabras, no importa donde se sitúe la fuerza en el cuerpo, siempre y cuando no se salga de su línea de acción. Debido a que el cuerpo se trata de forma ideal y no se deforma los sistemas son equivalentes.
Mover una fuerza por FUERA de su línea de acción
Una fuerza se puede mover por fuera de su línea de acción. Un error común es olvidar la tendencia de giro al desplazar la fuerza en otro punto del cuerpo, como se aprecia en la figura.
Estos dos sistemas no son equivalentes ya que el momento no se ha tenido en cuenta.
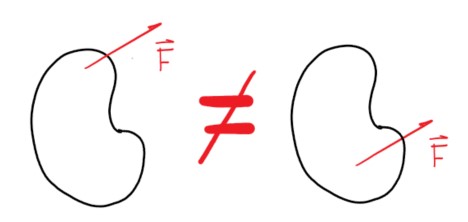

El sistema equivalente que se muestra en la figura es equivalente, quiere decir que es igual tener el cuerpo con la fuerza arriba que con la fuerza abajo y el momento.
Esto quiere decir que cada vez que se traslade una fuerza por fuera de su línea de acción debe aparecer un momento. El momento que se genera al trasladar la fuerza se obtiene por medio de la ecuación de momento alrededor de un punto:

El radio utilizado para calcular el momento que se genera al trasladar la fuerza debe iniciar en un punto de la línea de acción de la fuerza donde se va a trasladar y debe terminar en un punto de la línea de acción de la fuerza en la posición antes de trasladarse.
En la figura se muestran vectores en color verde, estos vectores son posibles opciones de radio. Las líneas en azul representan las líneas de acción de las fuerzas. Los vectores verdes inician en un punto de la línea de acción de la fuerza donde se va a situar. Estos vectores verdes terminan en un punto de la línea de acción de la fuerza antes de desplazarla. Cualquiera de estos vectores verdes se pueden utilizar, lo usual es utilizar un vector facil de determinar o que tenga pocas componentes.

Video explicativo: traslación de fuerza
En el siguiente video se explica porque al trasladar una fuerza por fuera de su línea se genera un momento. También se explica el uso de la ecuación de momento alrededor de un punto para calcular la tendencia de giro al trasladar la fuerza.