MOMENTO ALREDEDOR DE UN PUNTO
SISTEMAS EQUIVALENTES DE FUERZAS – EQUIVALENT SYSTEMS OF FORCES.
El momento de una fuerza se calcula como el producto vectorial entre la fuerza aplicada y el vector distancia que va desde el punto para el cual calculamos el momento (punto o eje de interés, para el cálculo de la tendencia de giro) hasta el punto en dónde se aplica la fuerza. Puede recibir el nombre de momento flector si el momento intenta flectar el cuerpo. También recibe el nombre de momento torsor (torque) si el momento intenta torcer el cuerpo.

Donde:
- M: es el vector del momento, la tendencia de giro. [unidades de fuerza distancia]
- F: es el vector de la fuerza [unidades de fuerza]
- R: es el vector del radio o distancia [unidades de distancia]. Inicia en el punto de interés y termina en un punto de la línea de acción de la fuerza.
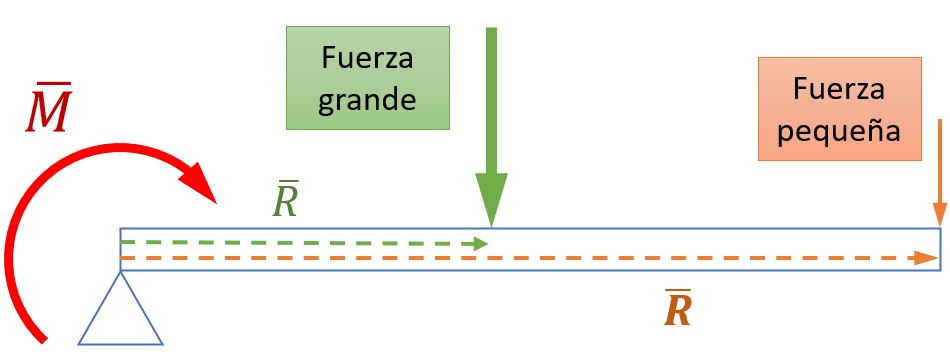
El momento al rededor de un punto representa la intensidad de la fuerza con la que se intenta hacer girar a un cuerpo rígido. El momento aumenta tanto si aumenta la fuerza aplicada como si aumenta la distancia desde el eje hasta el punto de aplicación de la fuerza. En otras palabras se puede producir el mismo momento con un radio pequeño y mucha fuerza (en color verde), que con un radio grande y poca fuerza (en color naranja).
Signo del momento en 2D

El signo del momento me indica la tendencia de giro. En la figura se observa para el primer caso un momento positivo, ya que el sentido de giro es contrario al sentido de las manecillas del reloj. En el segundo caso el sentido es negativo, ya que gira en el sentido de las manecillas del reloj. Es fácil determinar estos sentidos cuando se trabaja en el plano (2D), se puede determinar visualmente o utilizando la norma de la mano derecha.
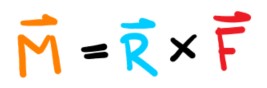
La regla de la mano derecha o del sacacorchos
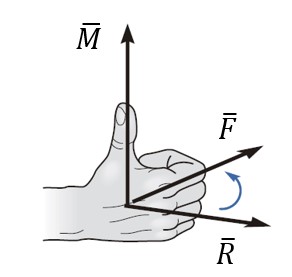
Es un método para determinar el sentido del vector, el cual podemos utilizar en el cálculo del momento. Si aplicamos la ecuación del momento, podemos poner nuestra palma de la mano derecha sobre el vector R, luego cerrar nuestro puño en el sentido del vector fuerza F y finalmente, estirar nuestro dedo gordo, el cual apuntará en el sentido del vector del momento M. El resto de dedos me muestra la tendencia de giro. Recordemos que el momento M es un vector perpendicular al plano formado por los vectores radio R y fuerza F.
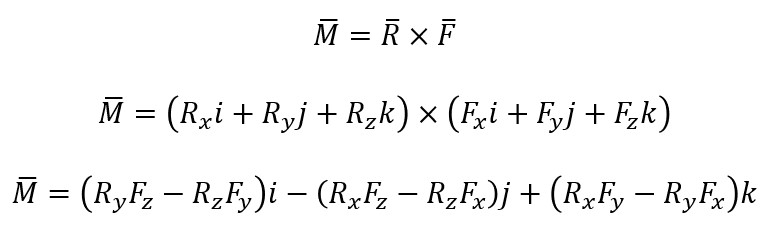
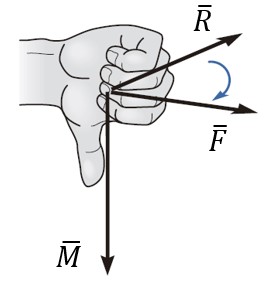
Momento en 2D
Cuando se trabaja en el plano, tanto el vector del radio como el vector de la fuerza tienen un máximo de dos componentes. Si el plano de trabajo es el xy, el momento solo tiene componente en el eje z.
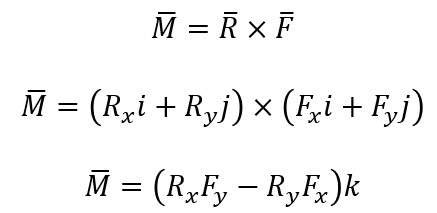
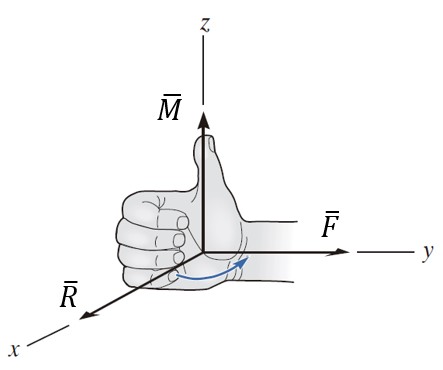
Por ejemplo, cuando los vectores del radio R y la fuerza F se encuentran en el plano xy, donde R tiene componente solo en el eje x y F componente solo en el eje y, el momento M producido por estos dos vectores se encuentra en el eje z.
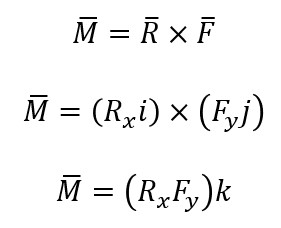
Módulo o norma del momento
Para determinar el módulo o la norma del momento, se puede realizar la raíz cuadrada de la cuadratura de cada una de sus componentes:
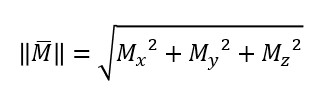
Pero en el plano es mas fácil determinarlo con la siguiente ecuación (también la puedo aplicar en el espacio):
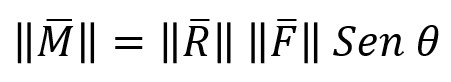
Recordemos que el producto cruz busca la perpendicularidad entre los vectores. Por tanto, cuando el ángulo θ = 90 grados el radio y la fuerza son totalmente perpendiculares y se puede multiplicar la magnitud del radio y la fuerza para obtener el momento.