CENTROIDES Y CENTROS DE GRAVEDAD
CENTROIDS AND CENTERS OF GRAVITY
¿QUÉ ES UN CENTROIDE?
En geometría, el centroide o baricentro de un objeto X perteneciente a un espacio n-dimensional es la intersección de todos los hiperplanos que dividen a X en dos partes de igual n-volumen con respecto al hiperplano. Informalmente, es el promedio de todos los puntos de X.

¿QUE ES EL CENTRO DE MASA?
El centro de masas de un sistema discreto o continuo es el punto geométrico que dinámicamente se comporta como si en él estuviera aplicada la resultante de las fuerzas externas al sistema. El centro de masas de un sistema de partículas es un punto que, a muchos efectos, se mueve como si fuera una partícula de masa igual a la masa total del sistema sometida a la resultante de las fuerzas que actúan sobre el mismo. Se utiliza para describir el movimiento de traslación de un sistema de partículas. Normalmente se abrevia como c.m. o G.
¿QUÉ ES EL CENTRO DE GRAVEDAD?
El centro de gravedad es el punto imaginario de aplicación de la resultante de todas las fuerzas de gravedad que actúan sobre las distintas porciones materiales de un cuerpo, de tal forma que el momento respecto a cualquier punto de esta resultante aplicada en el centro de gravedad es el mismo que el producido por los pesos de todas las masas materiales que constituyen dicho cuerpo.
En Física, el centroide, el centro de gravedad y el centro de masa pueden, bajo ciertas circunstancias, coincidir entre sí, aunque designan conceptos diferentes. El centroide es un concepto puramente geométrico que depende de la forma del sistema; el centro de masas depende de la distribución de materia, mientras que el centro de gravedad depende del campo gravitatorio.
Consideremos un cuerpo material:
- Para que el centroide del cuerpo coincida con el centro de masa, el cuerpo debe tener densidad uniforme, en otras palabras el material debe ser homogéneo e isotrópico.
- Para que un centro de masa del cuerpo coincida con el centro de gravedad, el cuerpo debe estar bajo la influencia de un campo gravitatorio uniforme.
Fuente: https://es.wikipedia.org/wiki/Centroide
PRIMER MOMENTO DEL AREA
Lo primordial para poder determinar el primer momento de área es saber que es, partiendo de esto se pude decir que en concreto el primer momento de área no es nada más que la distancia a la que se ubica una figura del origen o punto (0,0), los primeros momentos de área se determinan con respecto al eje X y respecto al eje Y, con respecto al eje X seria la distancia a la que se ubica una figura de dicho eje en dirección de Y y viceversa el primer momento de área con respecto al eje Y sería la distancia a la que se ubica la figura del eje Y con dirección en X.
Ahora que ya está definido en palabras claras que es un primer momento de área pasamos al siguiente punto, para que nos sirve, bueno la principal utilidad de estas medidas son el proporcionar información para determinar la ubicación del centroide de una figura.
Ahora lo más importante del tema, como determinar los primeros momentos de área, para esto utilizamos la siguiente formula:
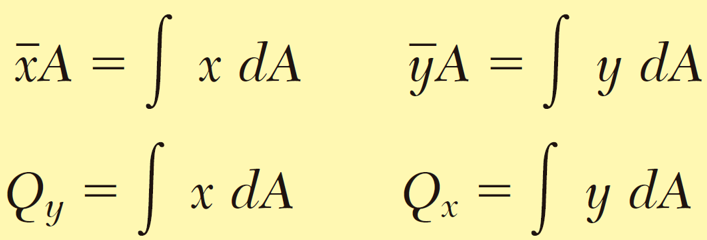
Dónde:
Qy = Primer momento de área con respecto al eje Y. Qx = Primer momento de área con respecto al eje X.
A = Área de la figura.
ẋ = Distancia entre el eje Y y la figura.
ẏ = Distancia entre el eje X y la figura.
En caso de tener un área no convencional, es decir formada por varias figuras, se aplica la misma fórmula para cada una de las figuras en el área.
Para determinar la ubicación del centroide de la figura solo se tiene que dividir los primeros momentos del área entre el área total de la figura, en el caso de una figura compuesta será la suma de los primeros momentos del área entre la suma de las áreas de las figuras que forman la figura principal. Esta operación se debe hacer dos veces una con el primer momento del eje X o la suma de estos, para determinar la coordenada en x y otra con el primer momento en Y o la suma de estos, para determinar la coordenada en y.
El primer momento de área es la distancia a la que se encuentra el cuerpo de cada una de los ejes principales o del origen.
Tabla de centroides y momentos de inercia.

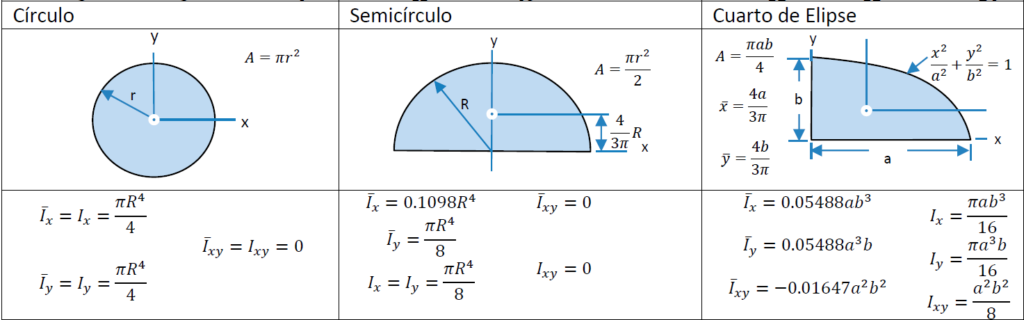
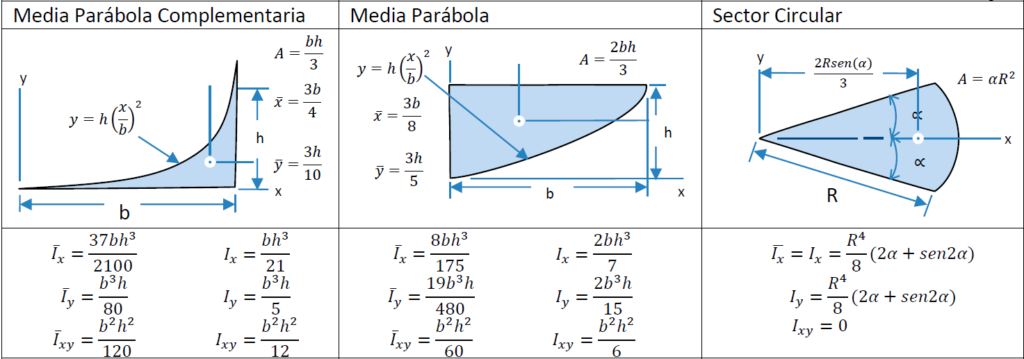

Ejemplo del uso de tabla para determinar el centroide
En el siguiente ejemplo se aprecia cómo se determina el centroide de la placa homogénea con espesor constante. Para esto se recurre al uso de la tabla de centroides y momentos de inercia publicada en esta página.
Ejemplo del cálculo del centroide por medio de integrales
En el siguiente ejemplo cómo la placa es homogénea con espesor constante, el centroide y centro de masa se encuentran ubicados en el mismo punto. En este caso se determina las coordenadas de este punto por medio de integrales.
Ejemplo, cómo calcular donde se concentra una carga distribuida
En el siguiente ejemplo se aprecia cómo se calcula la ubicación y valor de una fuerza concentrada generada por una carga distribuida utilizando centroides.
Ejemplo, fuerzas sobre superficies sumergidas
En el siguiente ejemplo se aprecia cómo a través del uso de centroides se calculan las fuerzas en diques y superficies sumergidas.
Ejercicios Resueltos
Ing. Mecánica ESTATICA - Hibbeler 14ta Ed
Ejercicios resueltos Capítulo IX: Centro de gravedad y centroide.