Ejercicios Resueltos CAPITULO 9 FUERZAS DISTRIBUIDAS: MOMENTOS DE INERCIA
Distributed Forces: Moments of Inertia – Beer & Jhonston, 9na Edición
A continuación se observa un listado de ejercicios resueltos del capítulo IX del libro Mecánica Vectoriar para Ingenieros ESTATICA – Beer, Jhonston, Mazurek & Eisenberg – 9na Edición.
Momentos de inercia por integración
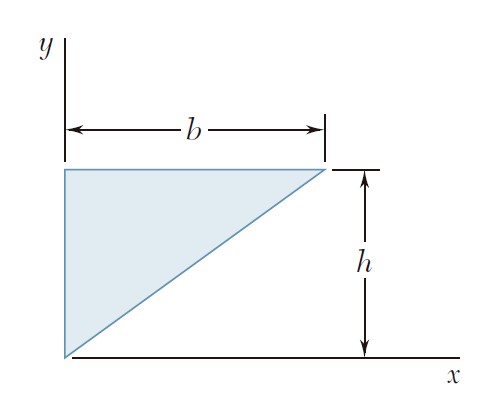
Ejercicio 9.1
Para el área sombreada que muestran las figuras, determine por integración directa el momento de inercia con respecto al eje y.
Ejercicio 9.2
Para el área sombreada que muestran las figuras, determine por integración directa el momento de inercia con respecto al eje y.
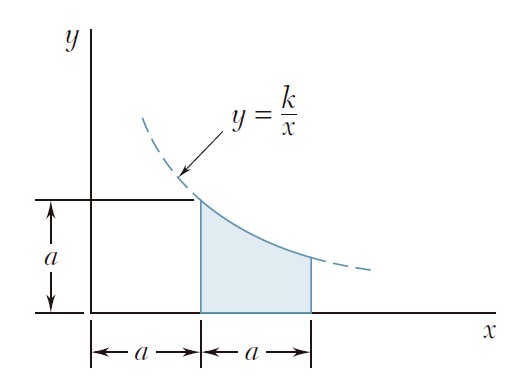
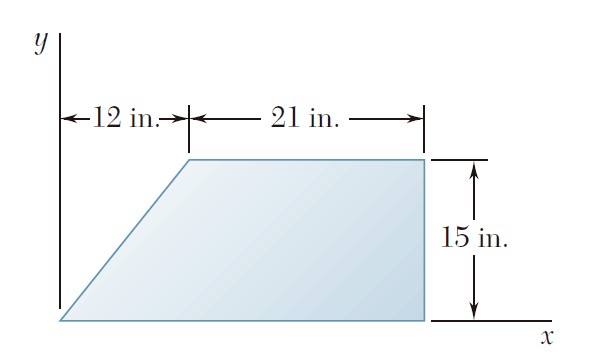
Ejercicio 9.3
Para el área sombreada que muestran las figuras, determine por integración directa el momento de inercia con respecto al eje y.
Ejercicio 9.4
Para el área sombreada que muestran las figuras, determine por integración directa el momento de inercia con respecto al eje y.
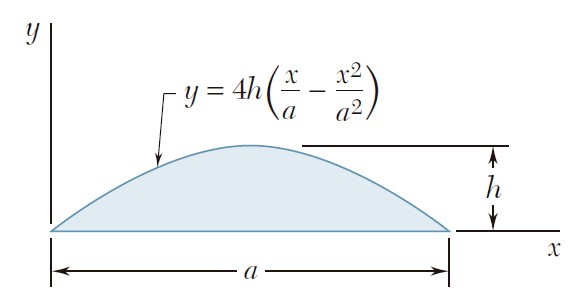
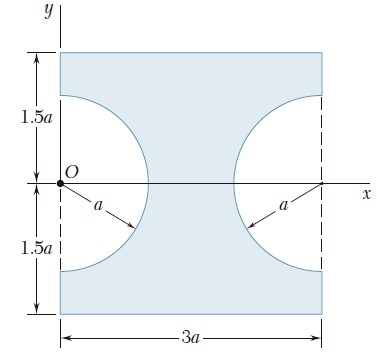
Ejercicio 9.5
Para el área sombreada que muestran las figuras, determine por integración directa los momentos de inercia con respecto al eje x.
Ejercicio 9.6
Para el área sombreada que muestran las figuras, determine por integración directa los momentos de inercia con respecto al eje x.
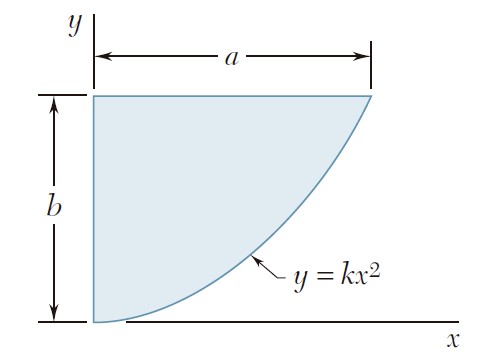
Ejercicio 9.7
Para el área sombreada que muestran las figuras, determine por integración directa los momentos de inercia con respecto al eje x.
Ejercicio 9.8
Para el área sombreada que muestran las figuras, determine por integración directa los momentos de inercia con respecto al eje x.
Ejercicio 9.9
Para el área sombreada que muestran las figuras, determine por integración directa el momento de inercia con respecto al eje x.
Ejercicio 9.10
Para el área sombreada que muestran las figuras, determine por integración directa el momento de inercia con respecto al eje x.
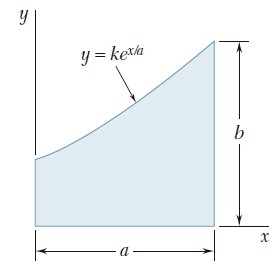
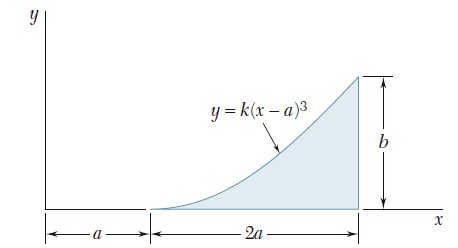
Ejercicio 9.11
Para el área sombreada que muestran las figuras, determine por integración directa el momento de inercia con respecto al eje x.
Ejercicio 9.12
Para el área sombreada que muestran las figuras, determine por integración directa los momentos de inercia con respecto al eje y.
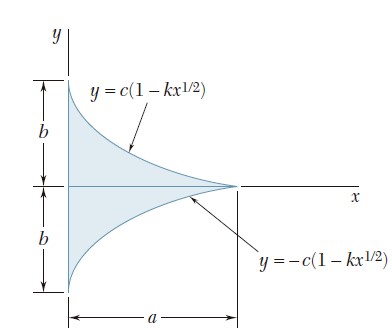
Ejercicio 9.13
Para el área sombreada que muestran las figuras, determine por integración directa los momentos de inercia con respecto al eje y.
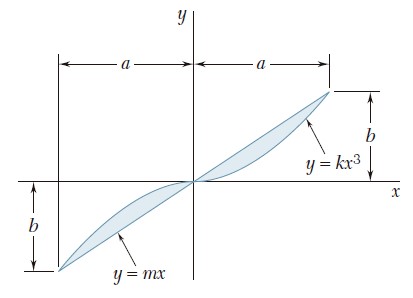
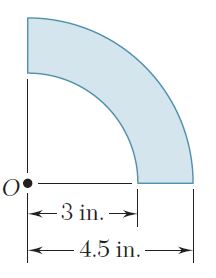
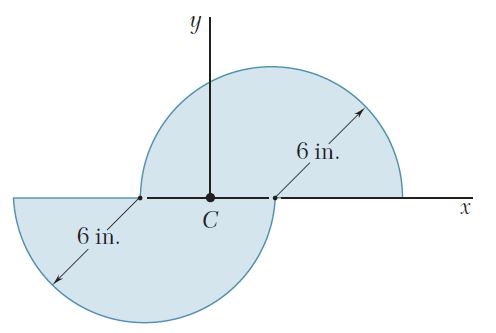
Ejercicio 9.15
Para el área sombreada que muestran las figuras, determine el momento de inercia y el radio de giro con respecto al eje x.
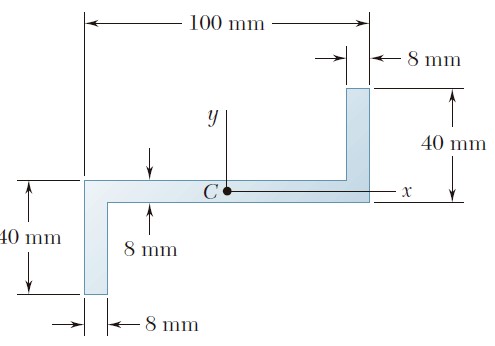
Ejercicio 9.16
Para el área sombreada que muestran las figuras, determine el momento de inercia y el radio de giro con respecto al eje x.
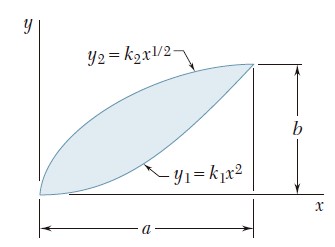
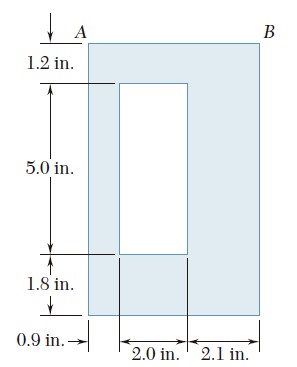
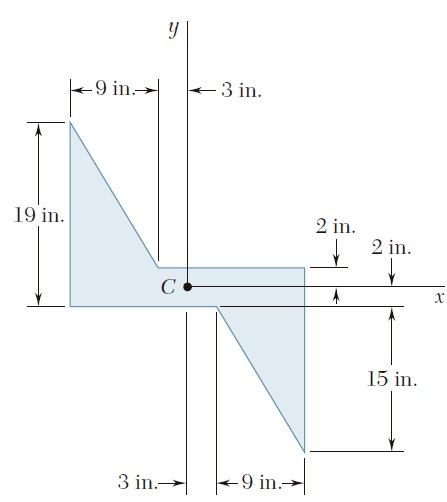
Ejercicio 9.17
Para el área sombreada que muestran las figuras, determine el momento de inercia y el radio de giro con respecto al eje y.
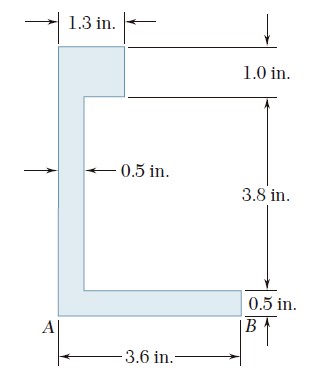
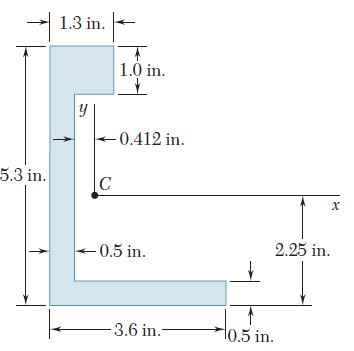
Ejercicio 9.18
Para el área sombreada que muestran las figuras, determine el momento de inercia y el radio de giro con respecto al eje y.
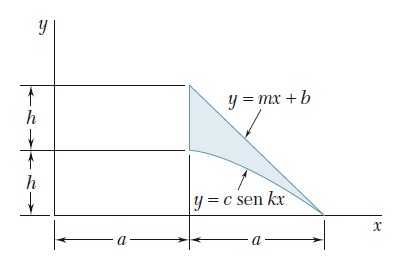
Ejercicio 9.19
Para el área sombreada que muestra la figura, determine el momento de inercia y el radio de giro con respecto al eje x.
Ejercicio 9.22
Para el área sombreada que muestran las figuras, determine el momento polar de inercia y el radio de giro polar con respecto al punto P.
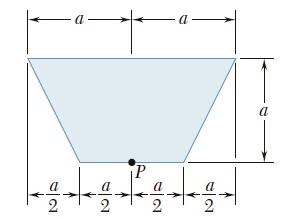
Ejercicio 9.26
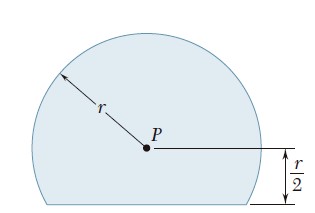
Para el área sombreada que muestran las figuras, determine el momento polar de inercia y el radio de giro polar con respecto al punto P.
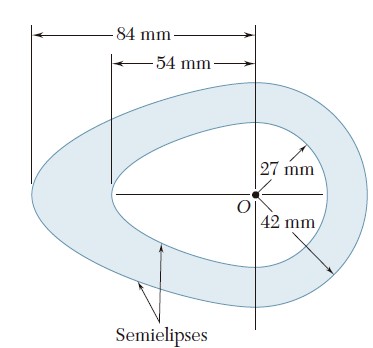
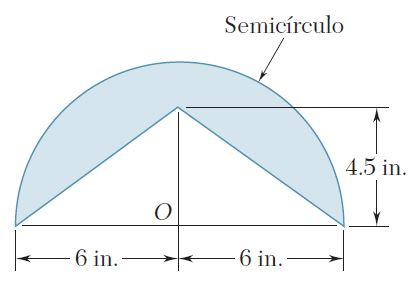
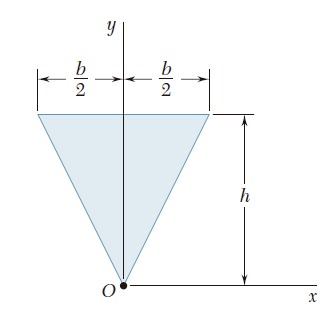
Ejercicio 9.28
Para el triángulo isósceles que muestra la figura, determine el momento polar de inercia y el radio de giro polar con respecto al punto O.
Momentos de inercia utilizando tabla
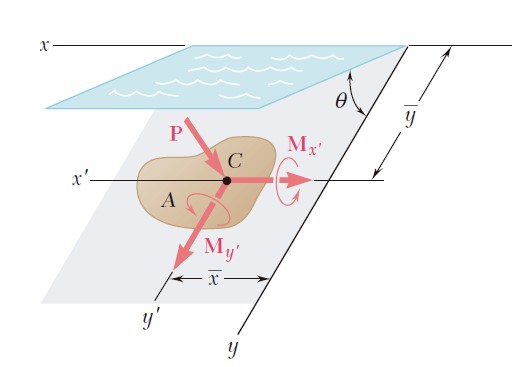
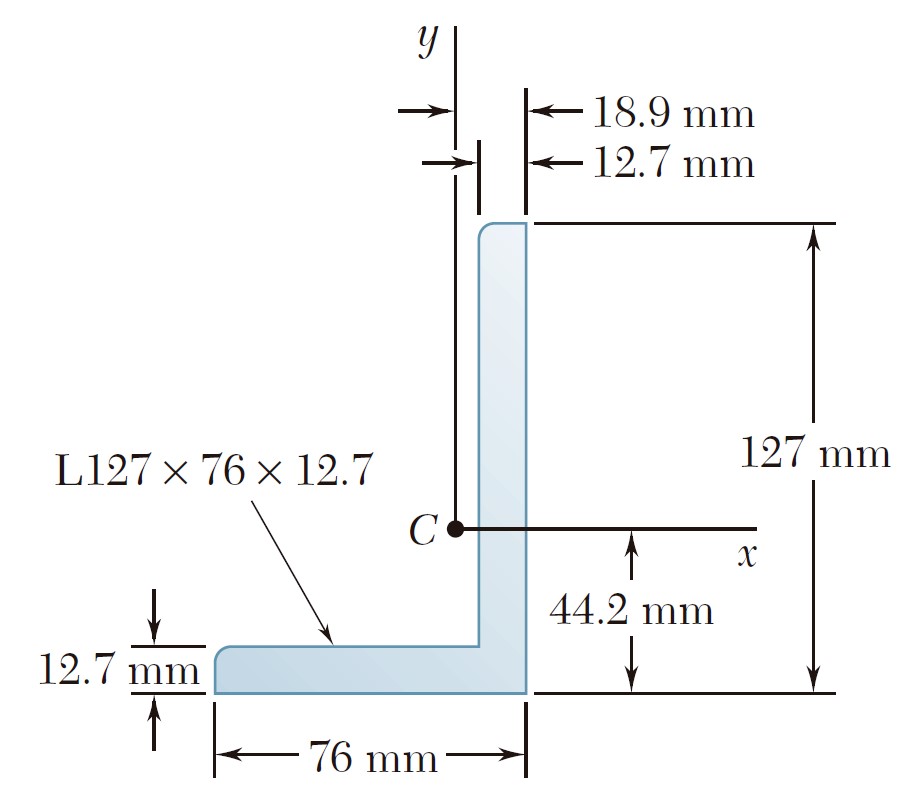
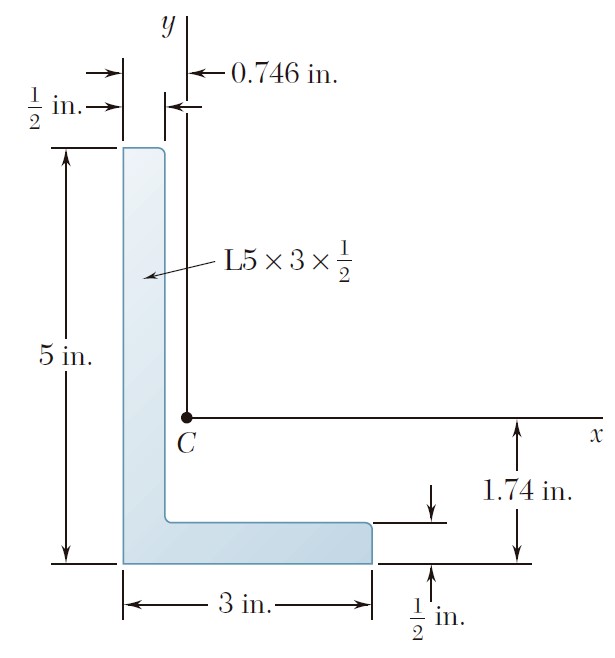
Ejercicio 9.65
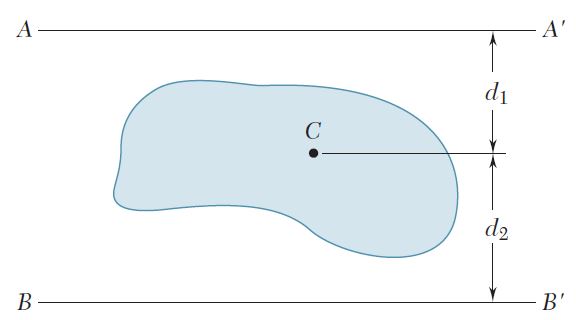
Demuestre que el sistema de fuerzas hidrostáticas que actúan sobre un área plana A que está sumergida, puede reducirse a una fuerza P sobre el centroide C del área y dos pares. La fuerza P es perpendicular al área y su magnitud es P = γ A y sen θ, donde γ es el peso específico del líquido y los pares son Mx’ = (γ Ix’ sen θ)i y My’ = (γ Ix’y’ sen θ)j, donde Ix’y’ = ∫x’y’ dA (vea la sección 9.8). Observe que los pares son independientes de la profundidad a la que está sumergida el área.
Producto de Inercia
Circulo de Morh
Problemas de rapaso
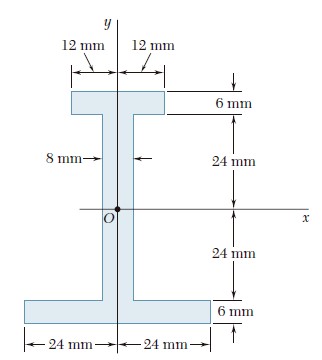
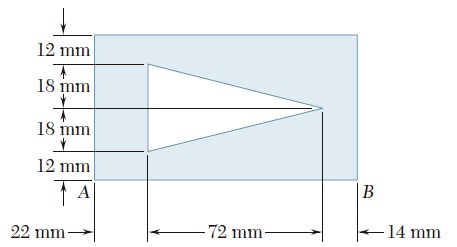
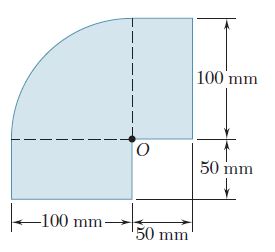
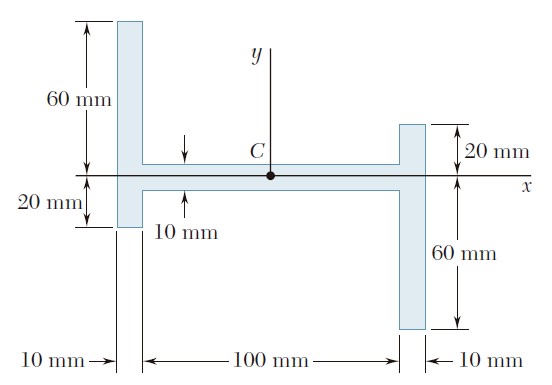
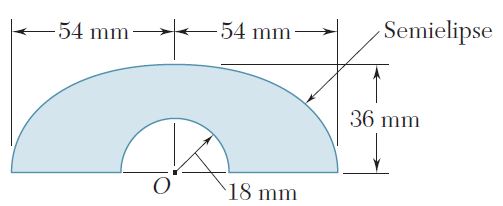
Ejercicio 9.188
Para el área sombreada que se muestra en la figura, determine los momentos de inercia con respecto a los ejes x y y.
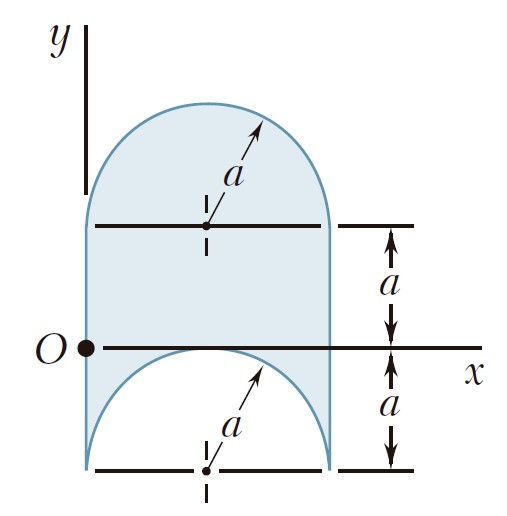
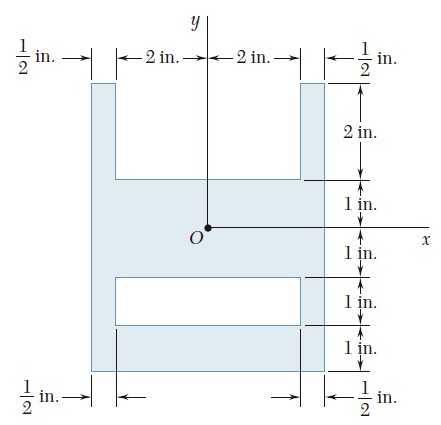
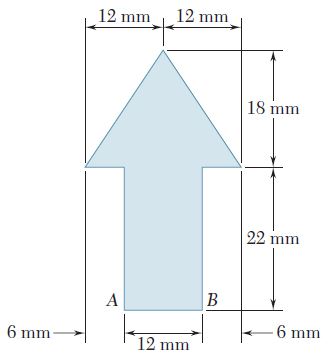
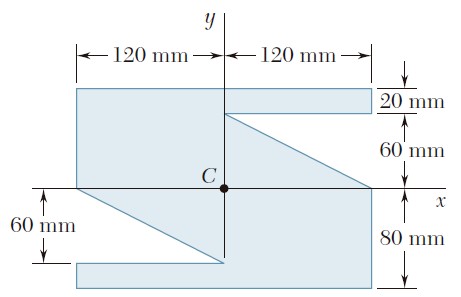
Para el área que se muestra en la figura, determine el momento polar de inercia con respecto a a) el punto O y b) el centroide del área.
Lista de ejercicios resueltos
– Momentos de inercia utilizando tabla
9.31 https://youtu.be/124AnPlizKs
9.32 https://youtu.be/2PEz0P3WYNA
9.33 https://youtu.be/_-CZ3re8ZRU
9.34 https://youtu.be/B4-9_Em4H-k
9.35 https://youtu.be/c_Zr5Zhs4x0
9.36 https://youtu.be/vJrqjnFlfpY
9.37 https://youtu.be/OFbEJx6yVRg
9.38 https://youtu.be/Ha2hzHm9Rbg
9.39 https://youtu.be/OqGYjjrWSTY
9.40 https://youtu.be/jmRMmFQxsUs
9.41 https://youtu.be/VYEmYwv6WeA
9.42 https://youtu.be/qLiVIdJGafc
9.43 https://youtu.be/fI6ExwYq8fY
9.44 https://youtu.be/Gd6SiezqqOY
9.45 https://youtu.be/_Q8D6jJT6Hg
9.46 https://youtu.be/rPX_YZPmd1s
9.47 https://youtu.be/NO1cnKkHwqs
9.48 https://youtu.be/c0v92VetHbU
9.49
– Producto de Inercia
9.67
9.71 https://youtu.be/t4T0parV-QM
9.72 https://youtu.be/b7Sbyv705vs
9.73 https://youtu.be/Ta5cMCqMIWU
9.74 https://youtu.be/rJnj36EJzpo
9.75 https://youtu.be/mkooPu9OtUA
9.76 https://youtu.be/NeuiQzxQFmc
9.77 https://youtu.be/82v2KIUYL58
9.78 https://youtu.be/ns5lQc9tkzs
– Circulo de Morh
9.93 https://youtu.be/Sa3I2QgCjJ8
– Problemas de rapaso
9.187
9.189 https://youtu.be/bjeIeDp7tvY
9.191 https://youtu.be/BGWgVPdFe8A
Mecánica vectorial para ingenieros. Beer, Johnston, Mazurek & Eisenberg. 9 Ed.
Mecánica vectorial para ingenieros. Beer, Johnston & Mazurek. 11 Ed.
