Ejercicios Resueltos CAPITULO 2 ESTÁTICA DE PARTÍCULAS
Beer & Jhonston, 9na Edición
A continuación se observa un listado de ejercicios resueltos del capítulo II del libro Mecánica Vectoriar para Ingenieros ESTATICA – Beer, Jhonston, Mazurek & Eisenberg – 9na Edición.
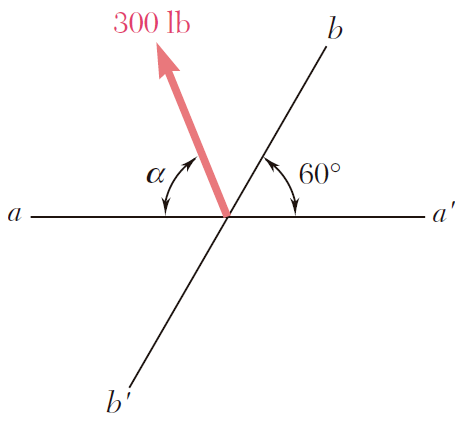
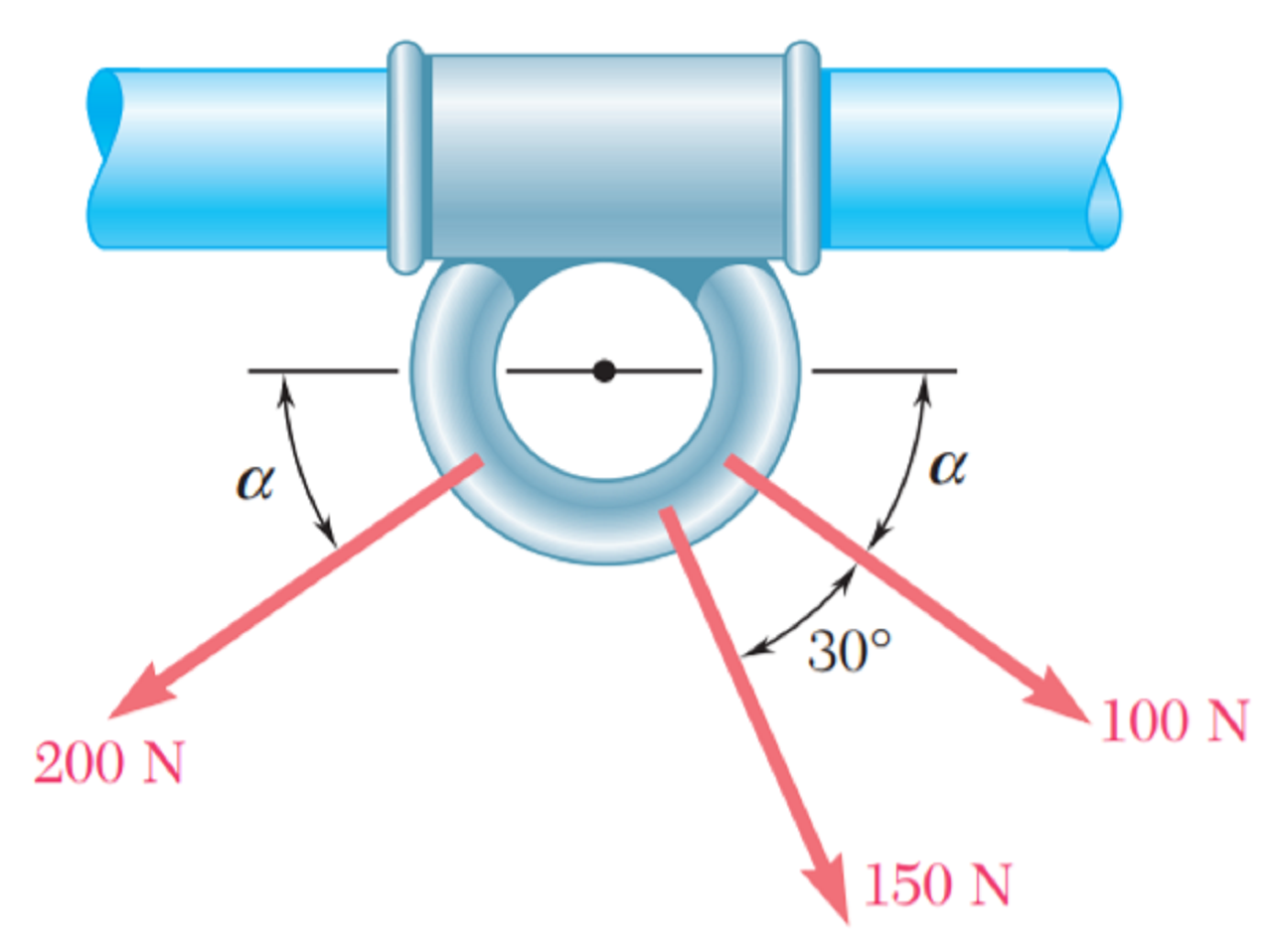
Suma de fuerzas 2D, ley del paralelogramo
Suma de fuerzas 2D, ley del paralelogramo
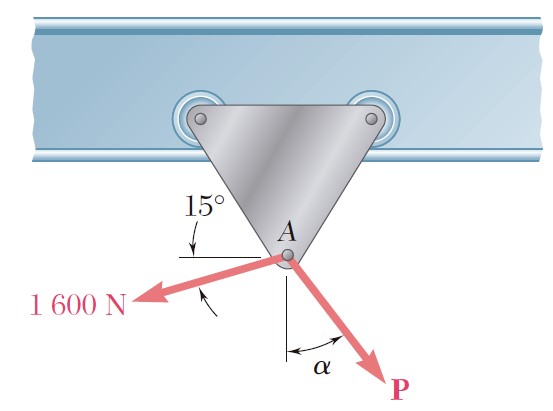
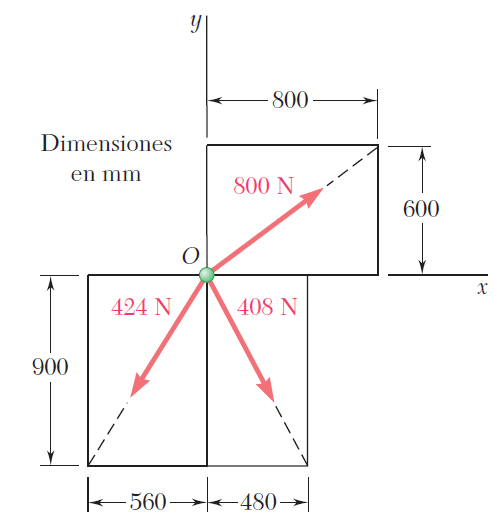
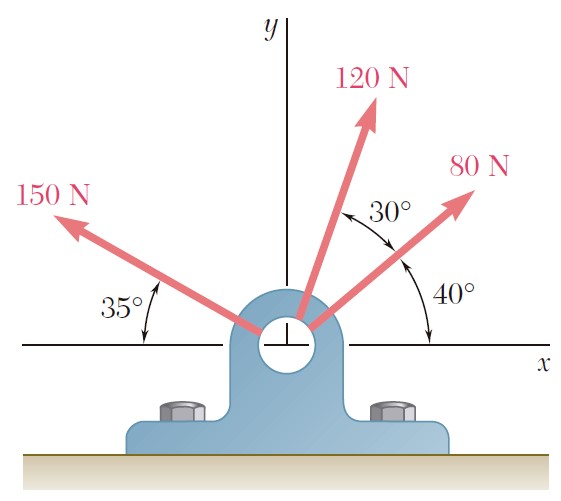
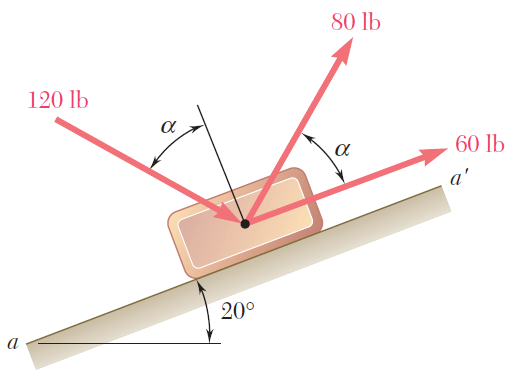
Suma de fuerzas 2D por componentes
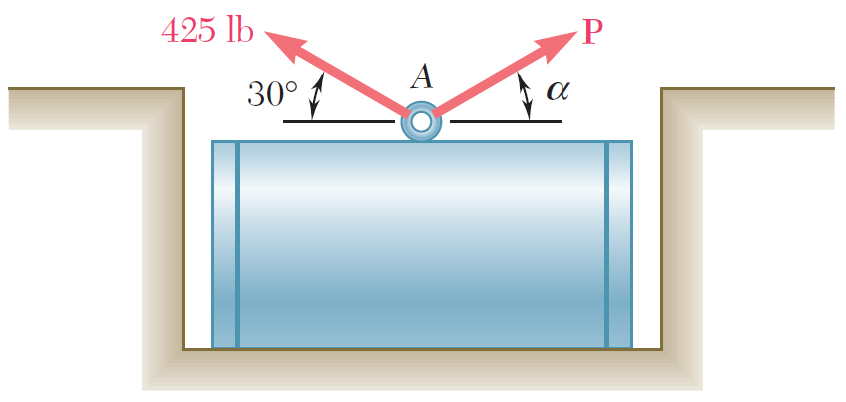
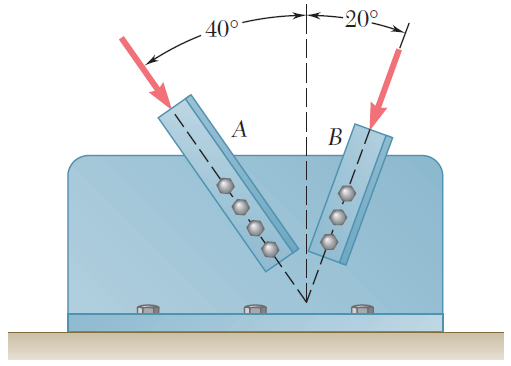
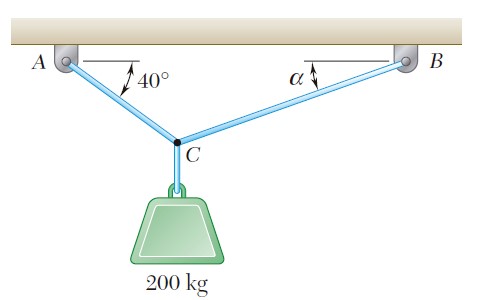
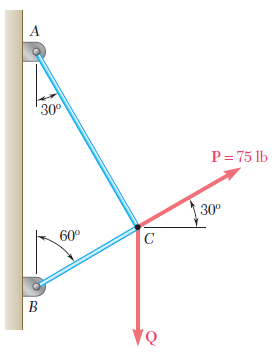
Equilibrio de una particula en 2D
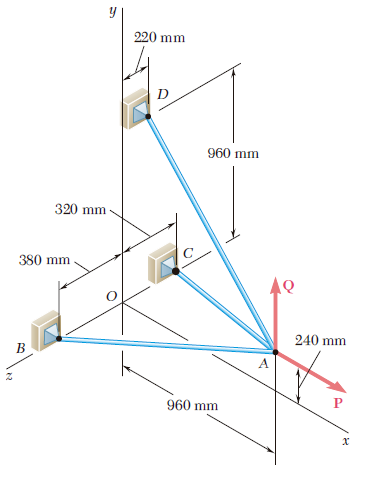
Ejercicio 2.69
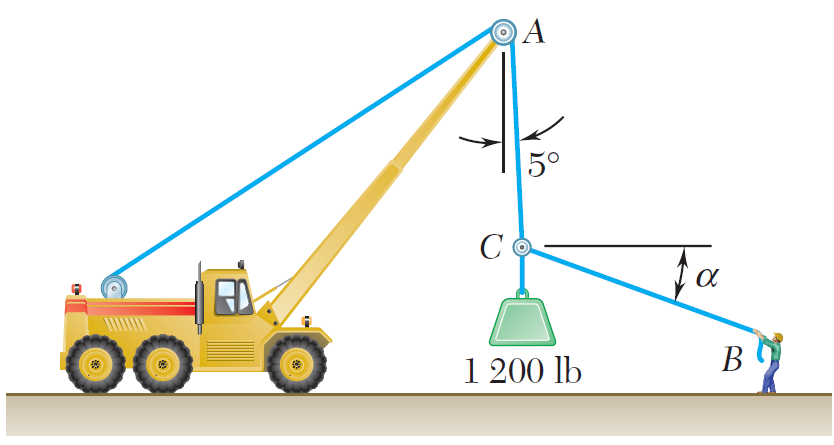
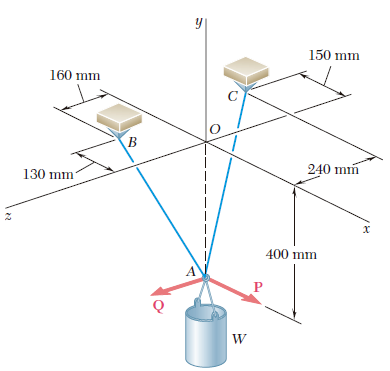
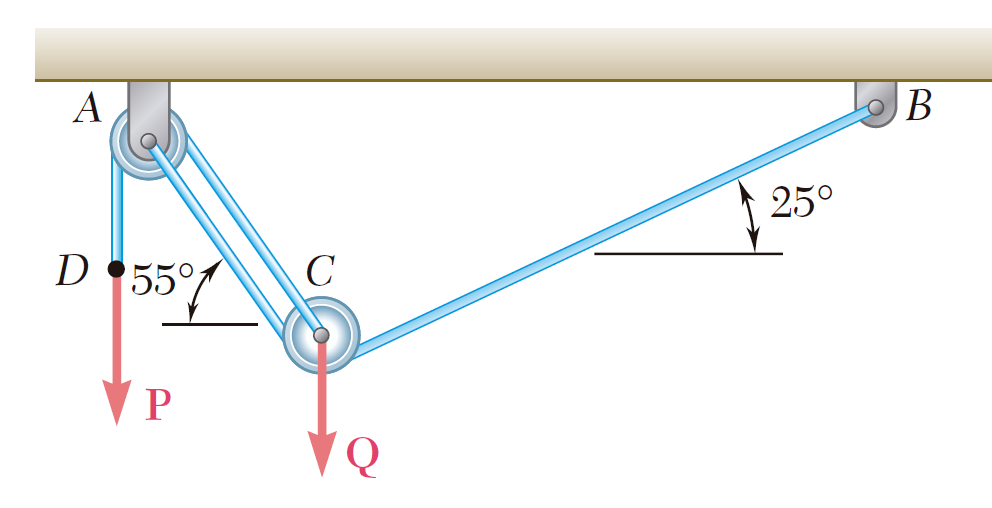
La carga Q se aplica a la polea C, la cual puede rodar sobre el cable ACB. La polea se sostiene en la posición mostrada en la figura mediante un segundo cable CAD, el cual pasa a través de la polea A y sostiene una carga P. Si se sabe que P = 750 N, determine a) la tensión en el cable ACB, b) la magnitud de la carga Q.
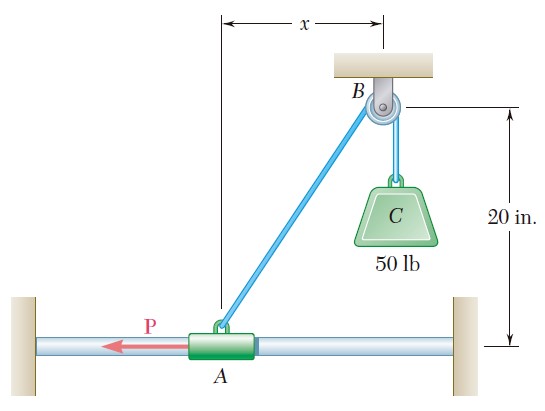
Ejercicio 2.70
Una carga Q de 1 800 N se aplica a la polea C, la cual puede rodar sobre el cable ACB. La polea se sostiene en la posición mostrada en la figura mediante un segundo cable CAD, el cual pasa a través de la polea A y sostiene una carga P. Determine a) la tensión en el cable ACB, b) la magnitud de la carga P.

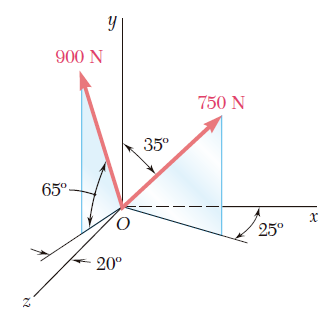
Cosenos directores de fuerzas en 3D
Ejercicio 2.82
Una fuerza actúa en el origen de un sistema coordenado en la dirección definida por los ángulos θy = 55° y θz = 45°. Si se sabe que la componente x de la fuerza es de –500 lb, determine a) el ángulo θx, b) las componentes restantes y la magnitud de la fuerza.La carga Q se aplica a la polea C, la cual puede rodar sobre el cable ACB. La polea se sostiene en la posición mostrada en la figura mediante un segundo cable CAD, el cual pasa a través de la polea A y sostiene una carga P. Si se sabe que P = 750 N, determine a) la tensión en el cable ACB, b) la magnitud de la carga Q.
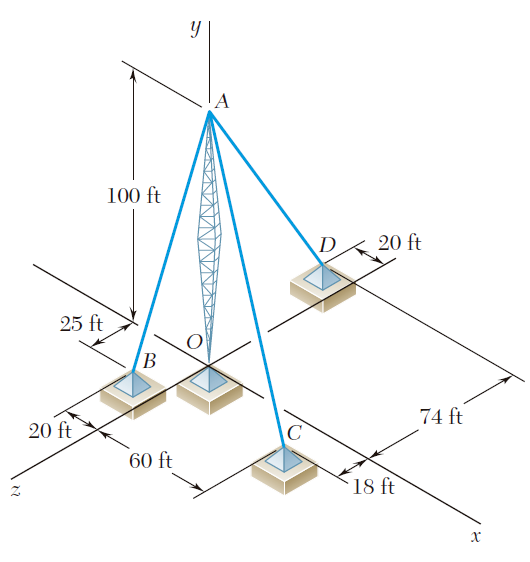
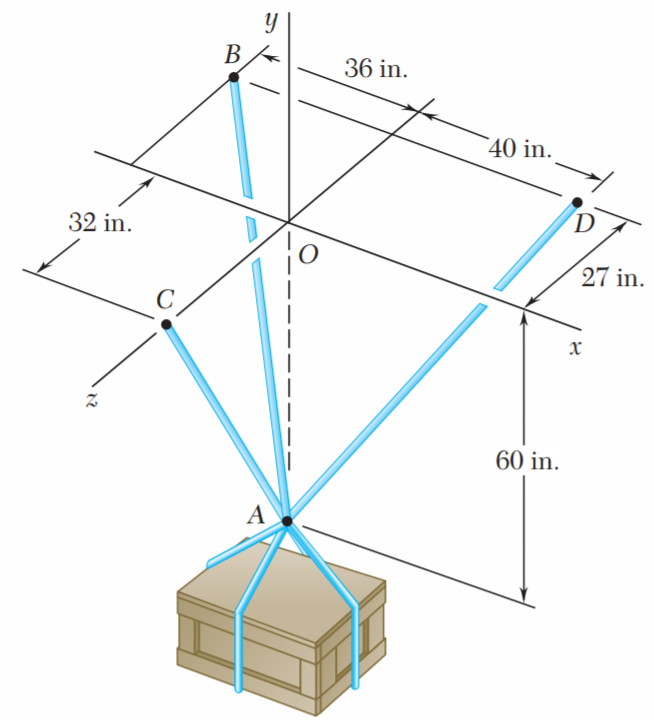
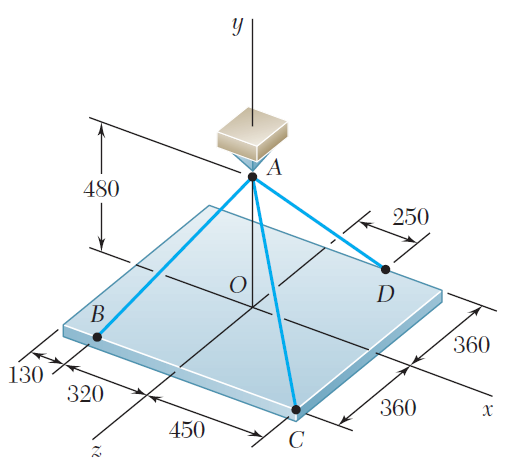
Ejercicio 2.84
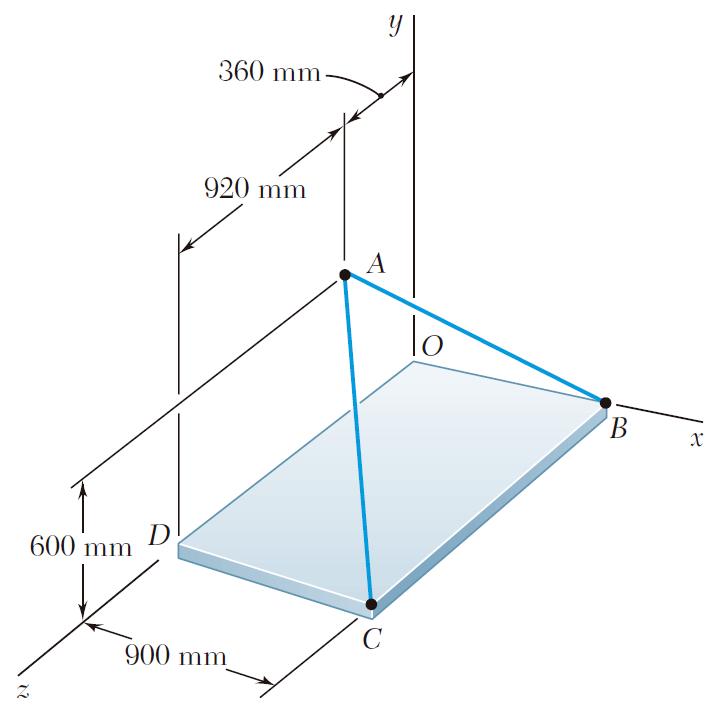
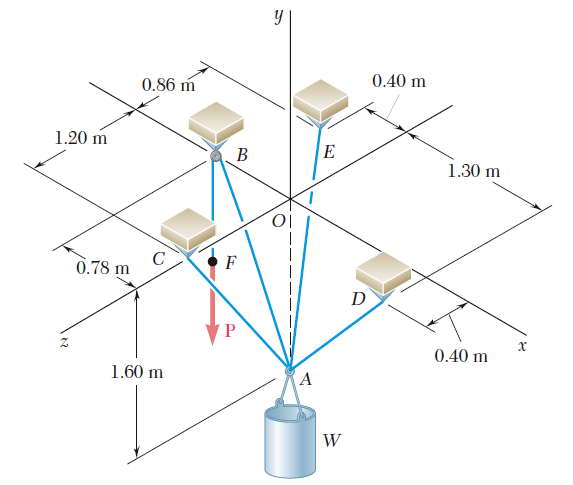
Una fuerza F de magnitud 230 N actúa en el origen de un sistema coordenado. Si se sabe que θx = 32.5°, Fy = -60 N y Fz > 0, determine a) las componentes Fx y Fz, b) los ángulos θy y θz.Una placa circular horizontal se sostiene mediante tres alambres que forman ángulos de 30° respecto de la vertical y se encuentran unidos a un soporte en D. Si se sabe que la componente x de la fuerza ejercida por el alambre AD sobre la placa es de 110.3 N, determine a) la tensión en el alambre AD, b) los ángulos θx, θy y θz que forma la fuerza ejercida en A con los ejes coordenados.
Componentes de fuerzas en 3D
Suma de fuerzas en 3D, Resultante
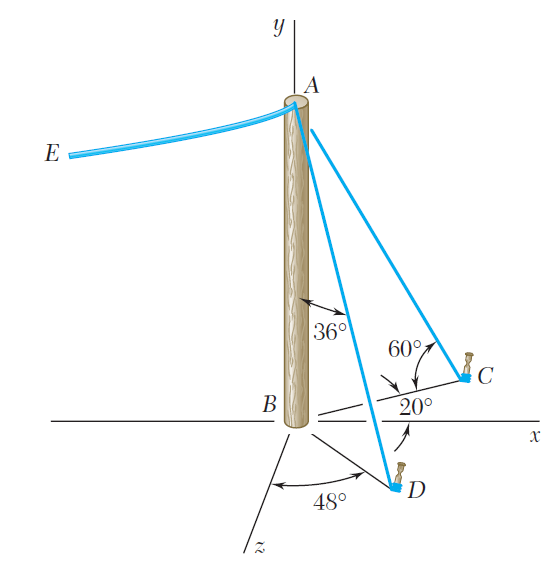
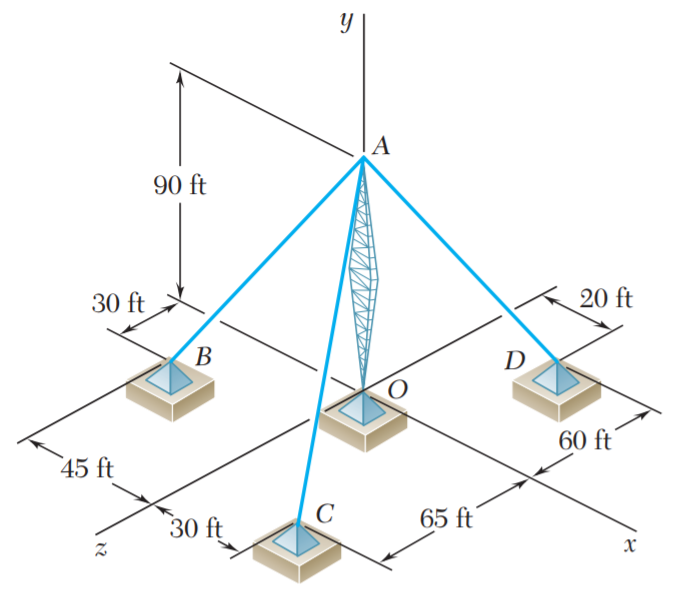
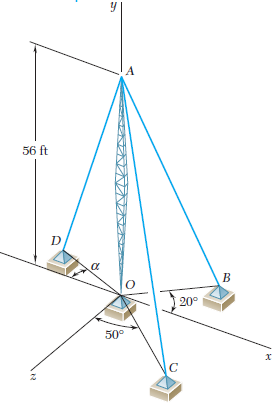
El extremo del cable coaxial AE se une al poste AB, el cual está
sostenido por los tirantes de alambre AC y AD. Si se sabe que la tensión en el alambre AD es de 125 lb y que la resultante de las fuerzas ejercidas en A por los alambres AC y AD debe estar contenida en el plano xy, determine a) la tensión en AC, b) la magnitud y la dirección de la resultante de las dos fuerzas.
Equilibrio de una partícula en 3D
Problemas de Repaso

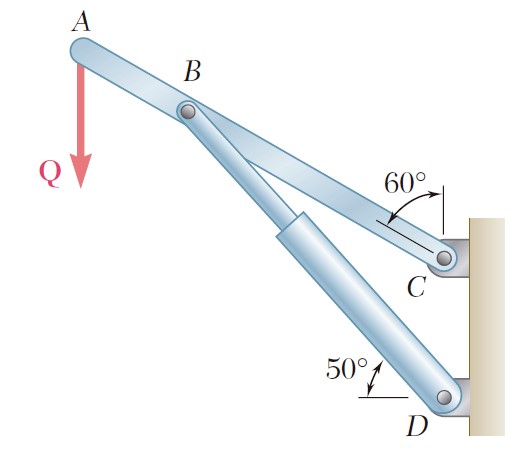
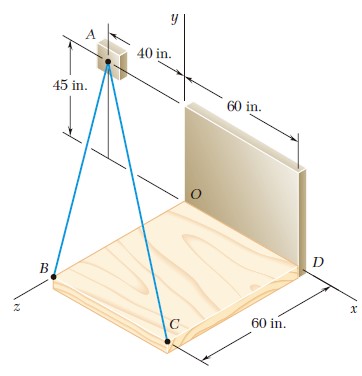
Ejercicio 2.129
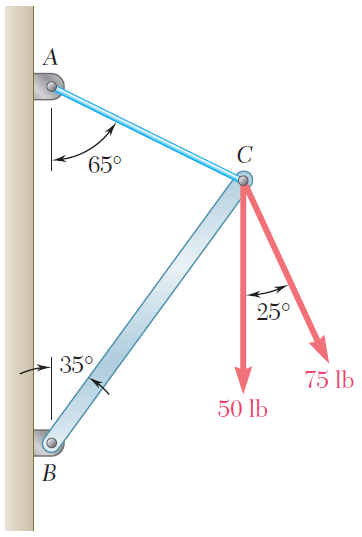
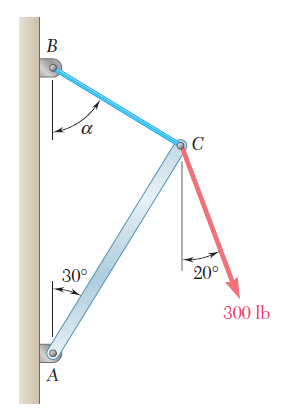
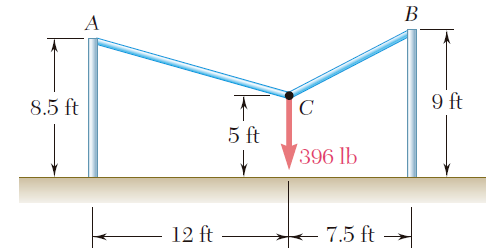
El elemento BD ejerce sobre el elemento ABC una fuerza P dirigida a lo largo de la línea BD. Si se sabe que P debe tener una componente vertical de 240 lb, determine a) la magnitud de la fuerza P y b) su componente horizontal.
Ejercicio 2.130
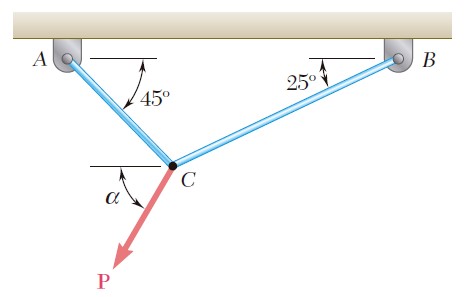
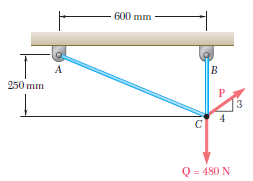
Dos cables se amarran en C y se cargan como se muestra en la figura. Determine la tensión a) en el cable AC y b) en el cable BC.

Ejercicio 2.135
A fin de mover un camión volcado, se atan dos cables en A y se jalan mediante las grúas B y C como se muestra en la figura. Si se sabe que la tensión en el cable AB es de 10 kN y en el cable AC es de 7.5 kN, determine la magnitud y dirección de la resultante de las fuerzas ejercidas en A por los dos cables.
Lista de ejercicios resueltos.
– Suma de fuerzas 2D, ley del paralelogramo
2.1 https://youtu.be/sDDG4xv957k
2.2 https://youtu.be/XY293NeMMso
2.3 https://youtu.be/h1q3GDJ4-kI
2.4 https://youtu.be/yxAQDYX-kGw
2.5 https://youtu.be/AxhiiWTyTLE
– Suma vectorial 2D, Ley de senos y cosenos
2.6 https://youtu.be/3y-O7dtIUyc
2.7 https://youtu.be/anKwCxdxVOU
2.8 https://youtu.be/a2eMSXh75Vc
2.9 https://youtu.be/C86S0nWBQjE
2.10 https://youtu.be/i1rUsiK3fiE
2.11 https://youtu.be/jbfcJjw1FXg
2.12 https://youtu.be/RYC-45EgklY
2.13 https://youtu.be/5oN5WVl-cBI
2.14 https://youtu.be/NdbYzcutxDg
2.15 https://youtu.be/CPU_isx-Mi4
2.16 https://youtu.be/p11UhgIbAfI
2.17 https://youtu.be/Zt_stD6ZFf0
2.19 https://youtu.be/S5SReroeky0
2.20 https://youtu.be/rAyX2ykR-X4
– Suma de fuerzas 2D por componentes
2.21 https://youtu.be/WzDjpfVI6js
2.22 https://youtu.be/2Fb2ZH_Qis0
2.23 https://youtu.be/Z7tDXTVF5jA
2.24 https://youtu.be/9wBx8zbg2GU
2.25 https://youtu.be/OlOuGrejcA4
2.26 https://youtu.be/E5vDQqQgQwA
2.28 https://youtu.be/1miXtFYMvOw
2.29 https://youtu.be/X5exEo2YQcU
2.30 https://youtu.be/zny78Fhrf78
2.31 https://youtu.be/LQf9Qq1OgQQ
2.32 https://youtu.be/9qjc2KVu8Sw
2.33 https://youtu.be/uHF8NCOutZw
2.34 https://youtu.be/WOpPGqBRm_Q
2.35 https://youtu.be/dPi59WUpW4A
2.36 https://youtu.be/iqtoHmFDUXo
2.37 https://youtu.be/vtiAtZod5n8
2.38 https://youtu.be/k_LQ_LVVDGA
2.39 https://youtu.be/BJSD01_40Kg
2.40 https://youtu.be/-3sdUPkiYQs
2.41 https://youtu.be/90eGGHdSJPc
2.42 https://youtu.be/ohKTShCl3qg
– Equilibrio de una particula en 2D
2.43 https://youtu.be/omAuHSk0dYA
2.44 https://youtu.be/–yxC-i-we8
2.45 https://youtu.be/g3oWXTW8Fpo
2.46 https://youtu.be/qLJMNe6JGXo
2.47 https://youtu.be/KqnYYO3sMvQ
2.48 https://youtu.be/iCOO7Gp5Yz0
2.49 https://youtu.be/0-LdXMt9bJA
2.50 https://youtu.be/KwiZj0dkfpI
2.51 https://youtu.be/g2XS56E1Zv4
2.52 https://youtu.be/ig1H0MZKlyI
2.53 https://youtu.be/DNbKrINTS4E
2.54 https://youtu.be/NXwNzQ_qpek
2.55 https://youtu.be/AnkXr4TtA5c
2.56 https://youtu.be/s32FmsIY6cI
2.57 https://youtu.be/oI1V38ZBRp0
2.58 https://youtu.be/1esNNMzvSlU
2.59 https://youtu.be/iqZmQnFL1GQ
2.60 https://youtu.be/eDRFUCJs_iE
2.61 https://youtu.be/SOfD-gMPwFc
2.63 https://youtu.be/cShZdQAECGk
2.64 https://youtu.be/JkWElZGvYJU
2.65 https://youtu.be/a30csYUQpPA
2.66 https://youtu.be/7adJGe2uT0o
2.67 https://youtu.be/5aku-l4VlV4
2.68 https://youtu.be/Ge51k9gglJI
2.70 https://youtu.be/aUORQ_nKbAI
– Cosenos directores de fuerzas en 3D
2.71 https://youtu.be/31mgc1MEPeE
2.72 https://youtu.be/yIxnK_HbEFI
2.73 https://youtu.be/FqlQFyOoNms
2.74 https://youtu.be/ls_VK7Evpjg
2.75 https://youtu.be/7RQS9yv500g
2.76 https://youtu.be/Cs-Crpqi69U
2.77 https://youtu.be/m3ziF4psZ0g
2.78 https://youtu.be/oXsoXctcDpY
2.79 https://youtu.be/zo8Rjs76LxE
2.80 https://youtu.be/HupiAGhiIOY
2.81 https://youtu.be/ckIp8LKKCY4
2.83 https://youtu.be/4AHoO55nvug
– Componentes de fuerzas en 3D
2.85 https://youtu.be/oq8rwnUF8gg
2.86 https://youtu.be/uC4P_PtoWPE
2.87 https://youtu.be/G1603KKKK_4
2.88 https://youtu.be/nQE744UD940
2.89 https://youtu.be/ufqfNuzoUVs
2.90 https://youtu.be/rooZqBoJ6Zk
– Suma de fuerzas en 3D, Resultante
2.91 https://youtu.be/Foyc4WGEgw0
2.92 https://youtu.be/EQt22uQVxmU
2.93 https://youtu.be/CRMVsuWIxP8
2.94 https://youtu.be/4n6lxyzGC-8
2.95 https://youtu.be/JZ8RWn7IuFw
2.96 https://youtu.be/xMQwWPBW_ZA
2.97 https://youtu.be/eE_mc-907rc
2.98 https://youtu.be/6_kU1fnsCzU
– Equilibrio de una partícula en 3D
2.99 https://youtu.be/y-nmHqz102s
2.100 https://youtu.be/pIv7Xd7qKCc
2.101 https://youtu.be/TBV4vnmgC6I
2.102 https://youtu.be/SGxTXAYepew
2.103 https://youtu.be/3TEhXeX5IDg
2.104 https://youtu.be/AZ3QbGAiurM
2.105 https://youtu.be/1gPrugYgsMs
2.106 https://youtu.be/ZwH–BjLDco
2.107 https://youtu.be/0jCjHDvNSA4
2.108 https://youtu.be/TQWWiOf3Jmo
2.109 https://youtu.be/XWEHLh8D6ic
2.110 https://youtu.be/sPfdeFxRuMQ
2.111 https://youtu.be/ebn7gGyU3Mw
2.112 https://youtu.be/-f4Go0ZlhhA
2.113 https://youtu.be/2zmmW-U-8IA
2.114 https://youtu.be/Jn5PhR627i8
2.115 https://youtu.be/wQrw68W4zR4
2.116 https://youtu.be/w8n41dv6s9c
2.117 https://youtu.be/WCfJrGfG2oU
2.118 https://youtu.be/U3Vvjkts1V8
2.119 https://youtu.be/eCzzVwdTceA
2.121 https://youtu.be/skq-fWJRJLk
2.122 https://youtu.be/zqiE0Twr_is
2.123 https://youtu.be/ZaZf5h8qnzc
2.124 https://youtu.be/ceemxW60rfQ
2.125 https://youtu.be/mGFgXqyHsu0
2.126 https://youtu.be/b6o8tAd1b7o
– Problemas de Repaso
2.127 https://youtu.be/enbo0easTH0
2.131 https://youtu.be/80P1fY6prF8